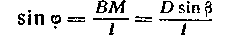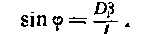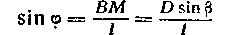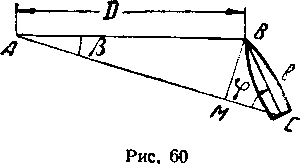
находится лодка, а ВС = / — длина корабля противника, то Z АСВ = <р называется курсовым углом корабля ВС. Дистанцию АВ попрежнему будем обозначать через D и будем считать длину корабля I малой по сравнению с расстоянием D. Пусть ВМ J. АС. Тогда

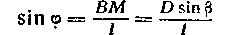М

и, вследствие малости угла р,

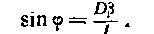(8,3)

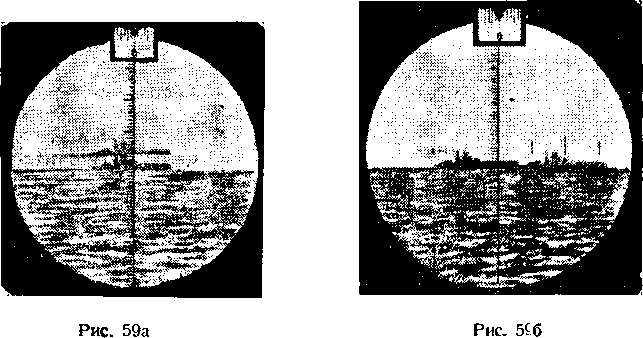
Для измерения угла (J, всегда расположенного приблизительно в горизонтальной плоскости, пользуются тем же микрометром, который при определении дистанции служит для измерения вертикального угла а. Однако теперь разведение двух изображений цели нужно производить не по высоте, а по горизонтальному направлению, для чего микрометр поворачивают, как целое, на угол 90° вокруг оптической оси. Измерительным валиком микрометра нужно развести два изображения так, чтобы нос наблюдаемого корабля в одном изображении коснулся кормы его во втором изображении (рис. 596).

Оптические части микрометра, вызывающие двоение изображения, монтируются на перископе таким способом, что их по желанию наблюдателя можно поворачивать на прямой угол вокруг оптической оси перископа. После

измерения расстояния достаточно лишь повернуть микрометр на угол 90°, чтобы можно было приступить к измерению курсового угла.

Микрометры предназначаются, как правило, для употребления при большом увеличении перископа, потому что, вследствие больших размеров изображения цели, в этом случае получается ббльшая точность измерения.

Зная угол р, под которым видна цель, по формуле (8,3) вычисляют курсовой угол <р; можно для этого воспользоваться также заранее составленными таблицами или номограммами. Для ускорения и упрощения процесса получения величины удаления цели и ее курсового угла прибегают к механическому способу решения соответствующего измерительного треугольника ABC. Микрометр усложняют, снабжая его несколькими подвижными шкалами, нанесенными на круглых кольцах. Часть из них передвигается автоматически при вращении измерительного маховичка, т. е. в зависимости от получаемой величины разведения двух наблюдаемых изображений. Другие шкалы можно передвигать от